Volume Rendering에 대해서 알아보고자 한다.
Volume Rendering을 3D 데이터를 렌더링(시각화) 하는 하나의 방식이다. 볼륨 렌더링은 그러면 어떤 데이터를 렌더링 하는 것인가? 우리가 기본적으로 사용하는 3D 데이터들은 다음과 같다.
메시(Mesh)
메시는 가장 일반적인 3D 모델링 방식으로, 내부가 비어 있으며 3D 오브젝트의 형상을 다각형(Polygon)으로 표현하는 방식이다. 우리가 흔히 접하는 영화나 게임의 3D 그래픽 객체들은 대부분 이 방식으로 제작된다.
메시는 폴리곤(Polygon)을 기반으로 구성되며, 각 폴리곤에는 다음과 같은 속성이 포함된다.
• 법선 벡터(Normal Vector): 표면의 방향을 나타내어 빛 반사와 음영(Shading)에 영향을 준다.
• 텍스처(Texture): 오브젝트 표면에 입혀지는 이미지로, 현실적인 질감을 표현하는 데 사용된다.
• 재질(Material): 반사도, 광택, 굴절률 등의 특성을 결정하는 요소이다.
3D 게임이나 영화에서 사실적인 그래픽을 구현하기 위해 더 많은 폴리곤을 사용하게 되는데, 이는 곧 연산량 증가로 이어진다. 폴리곤이 많아질수록 각 폴리곤에 대한 조명, 반사, 그림자 효과 등을 계산해야 하므로 그래픽 연산의 부하가 상당히 커지게 된다. 특히, 최신 3D 게임들은 더욱 정밀한 디테일과 사실적인 광원 효과를 구현하기 위해 수백만 개 이상의 폴리곤을 사용하므로, 이러한 연산을 실시간으로 처리하려면 고성능 그래픽 카드(GPU)가 필수적이다.
포인트 클라우드(Point Cloud)
포인트 클라우드는 3D오브젝트를 점들의 집합으로 표현하는 방식이다. 내부가 비어있고 경계를 표현한다는 점에서 메시와 닮아있지만 표면이 아닌 점으로 표현한다는 점에서 차이점을 가지고 있다. 주로 LiDAR(Light Detection and Ranging)와 같은 3D 스캐닝 센서들을 통해서 데이터가 생성되며 자율주행이나 도시나 건물등의 3D 모델링에 주로 쓰인다. 점들의 위치에 대한 정보밖에 없기 때문에 3D 객체에 효과적용이나 렌더링 적용 시 메시 등으로 변환하는 과정을 거친다.

그렇다면 볼륨 렌더링은 이 중 어떤 데이터에 쓰이는 기법일까? 결론은 둘다 아니다. 위키피디아에 의하면 "3차원 스칼라 장 형태의 이산 샘플링 데이터"에 적용된다고 한다. 도대체 이게 무엇을 의미하는 것일까?
3차원 스칼라 장 형태의 이산 샘플링 데이터?
3차원 스칼라 장 ?
- 3D공간의 각 위치에서 특정한 "스칼라 갑(Scalar Value)"이 정의된 데이터 필드를 의미
- 즉, 3D공간 내의 모든 점이 하나의 숫자(스칼라 값)를 가짐
이산 샘플링 데이터?
- 현실에서는 3D공간을 무한히 연속적으로 측정할 수가 없음
- 대신, 일정한 간격으로 데이터를 샘플링하여 저장해야 함
- 3D공간의 스칼라 값을 이산적인(Discrete) 격자(Grid)형태로 샘플링 한 데이터
우리가 흔히 평면에 여러 점들로 구성된 이미지를 픽셀(pixel)이라 부르듯이, 3D 공간에 표현된 단위 요소를 복셀(Voxel)이라고 하는데 복셀이 이에 해당된다고 할 수 있다(마인크래프트의 블록을 생각하면 이해가 쉬울것이다). 일상적인 예로는, MRI나 CT 스캔 이미지처럼 연속적인 인체 데이터를 샘플링하여 저장하는 경우가 이에 해당한다고 볼 수 있다.

그럼 해당 데이터로 어떻게 3D표현을 할 수 있을까? 가장 단순하게는 그냥 해당 데이터들을 하나씩 그려서 쌓아줄 수 있겠다. 해당 방식을 Texture Slicing이라고 하며 가장 기본적인 Volume redering의 방법이다.

x, y, z 축 방향으로 샘플링 된 데이터를 축의 방향대로 쌓아올렸다. 해당 방향으로 본다면 3D이미지 처럼 보이게 될 것이다 그런데 샘플링된 단면적 쪽을 바라본다면 어떻게 될까? 이미지가 그려지지 않는다. 투명한 아크릴 판을 여러개 쌓아올려 입체적인 풍경 그림을 그린다고 가정해보자. 해당 그림을 그린 방향대로 앞에서 본다면 분명 아래와 같은 입체적인 풍경화가 될테지만 옆에서 바라본다면? 어떠한 그림인지 알 수 있겠는가?

따라서 보는 데이터가 방향대로 쌓아올려져 있어야 우리에게 의미있는 이미지가 된다고 할 수 있다. 따라서 나오게 된 것이 View-aligned slice 방식이다, 기존에 데이터가 샘플링된 단면의 방향이 아닌 우리가 보는 방향과 수직이 되도록 단면을 내는 것이다. 당연히 데이터는 해당 방향 외에 값에 단면에 대해서는 정의되어 있지 않기 때문에 방향이 바뀔때마다 추가적으로 계산해줘야 하며, 실제로 샘플링된 방향에서의 결과물과에도 퀄리티 차이가 생기는 문제가 발생하게 된다. Slicing을 사용한 방식에는 이러한 한계점들 있었기 때문에 Volume ray-casting이라는 새로운 렌더링 기법이 등장하게 되었다
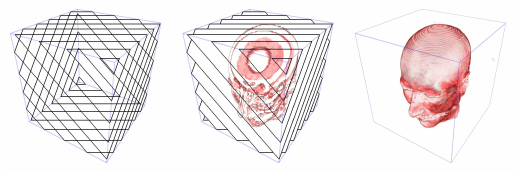
Volume ray-casting
volume ray-casting을 이해를 돕기 위해 그래픽스의 ray-casting 개념에 대해서 잠깐 설명하겠다.
우리는 눈으로 들어오는 빛에 의해서 시각으로 인지한다. 따라서 우리가 보는 모든것이 빛에 의한 반사에 의하여 보는 것이라고도 말할 수 있다. 우리가 이것을 가상으로 구현한다고 하면 광원(햇빛, 조명 등)에 의한 빛과 반사되는 수많은 빛에 대하여 모두 계산해야 될 것이다. 이는 사실상 불가능하다.
그렇기 때문에 그래픽스에서는 우리 눈에 들어오는 빛에 대해서만 계산하는 방식을 사용하게 된다. 보는 방향으로 들어오는 빛에 대해서만 계산하기 위해서, 오히려 해당 방향으로 빛을 내보낸다고 가정하고, 해당 방향에서 발생하는 추가적인 효과들(반사, 굴절 등)을 생성하는데 이것이 바로 Ray-casting이다. 그리고 이를 역으로 추적하는 과정을 Ray-tracing이라고 한다.
Volume ray-casting이 가지는 차이점은 표면만 존재하는 메쉬형태의 데이터가 아닌 3D 스칼라장 어쩌구 볼륨 데이터에 적용된다는 점이다. Slicing은 단면을 하나씩 쌓아올리는 식으로 렌더링이 이루어졌다. 그렇다면 ray-casting은 어떤식으로 이루어질까?

위 그림은 Volume ray-casting의 과정을 간단하게 나타낸 그림이다. 여기서 Image Plane은 우리가 보는 방향에 최종적으로 렌더링 되어 보여질 2D이미지를 의미하고 Image Plane으로 부터 3D 데이터까지 이어져있는 여러 선들이 보내는 빛을 의미한다. 이제 해당 과정을 단계별로 살펴보자.
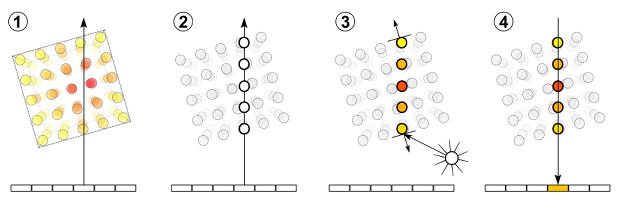
1. 광선(ray) 생성
- 보는 방향(Image Plane)에서 볼륨데이터를 향하는 광선(ray)을 보낸다
2. 샘플링
- 광선을 따라 설정한 간격에 따라 해당 위치의 데이터값(색상, 밀도)을 샘플링한다.
- 광선이 지나가는 위치에 정확히 데이터가 존재하지 않는 경우는?
-> 인접 데이터값들을 사용해 보간한 값을 이용한다
3~4. 최종 색상 계산
- 각 샘플의 밀도와 거리를 고려하여 최종 픽셀의 색상을 계산한다
-> 투명도(opacity) / 투과도(transmittance)가 반영된 이미지가 만들어지게 된다 - 필요에 따라서 추가적인 광원을 배치하고 효과를 계산해 좀 더 현실적인 이미지를 생성할 수도 있다
최종 색상은 다음과 같은 수식을 통해 계산된다.
$$C(x) = \sum_{i} T_i \cdot (1 - \exp(-\sigma_i \delta_i)) \cdot c_i$$
• $C(x)$ : 최종 픽셀 색상
• $\sigma_i$ : i 번째 샘플 위치의 밀도 (𝜎)
• $\delta_i$ : 샘플 간 거리(Δt)
• $c_i$ : i 번째 샘플의 색상 (RGB)
• $T_i$ : 누적 투과율 (이전 샘플들을 지나면서 얼만큼 빛이 통과되었는지)
• $(1 - e^{-\sigma_i \delta_i})$ : 현재 샘플이 빛을 흡수하는 양 (opacity)
volume ray-casting을 통한 랜더링은 투과율을 사용하는것이 핵심이다. 여기서 투과율(Transmittance)은 빛이 어떠한 매질(Volume)을 통과할 때, 밀도에 따라 얼만큼 통과되는지를 나타내는 값이다. 밀도가 높은(𝜎가 큰) 영역을 지나면, 빛이 많이 흡수되어 투과율이 낮아질 것이고, 밀도가 낮은(𝜎가 작은) 영역을 지나면, 빛이 덜 흡수되어 투과율이 높게 유지될 것이다. 이를 색상과 조합해 샘플링 된 모든 값을 더하면 최종 색상이 계산되게 된다. 이해를 위해 간단한 예제를 하나 만들어봤다.
예제 (Volume ray-casting)
- 광선(Ray)가 5개의 샘플 위치를 지나면서 색상과 밀도값을 샘플링한다고 가정하자
- 각 샘플 위치에서 밀도(𝜎)와 색상(RGB)는 다음과 같다
| 샘플링 위치 | 밀도(𝜎) | 색상(RGB) | 거리(Δt) |
| t1 | 0.2 | (255,0,0) (빨강) | 0.5 |
| t2 | 0.4 | (0,255,0) (초록) | 0.5 |
| t3 | 0.8 | (0,0,255) (파랑) | 0.5 |
| t4 | 0.3 | (255,255,0) (노랑) | 0.5 |
1. 투과율(Transmittance) 계산
$$T_i = T_{i-1} \cdot e^{-\sigma_{i-1} \cdot \delta_{i-1}}$$
• $(e^{-\sigma_j \delta_j})$ : 현재 샘플의 투과율
• $T_i$ : 누적 투과율 (이전 샘플까지 고려한 누적된 투과율)
투과율의 초기값 $T_0$은 1.0이다 (샘플을 만나기 전 광선)
| 샘플링 위치 | 투과율($T_i$) |
| t1 | $1.0 \times e^{-0.2 \times 0.5} \approx 0.90$ |
| t2 | $0.90 \times e^{-0.4 \times 0.5} \approx 0.71$ |
| t3 | $0.71 \times e^{-0.8 \times 0.5} \approx 0.44$ |
| t4 | $0.44 \times e^{-0.3 \times 0.5} \approx 0.38$ |
2. 불투명도(Opacity) 계산
- 현재 샘플에서 빛이 얼마나 투과되지 않는지를 나타냄
- 빛을 많이 투과 안될수록 (불투명도가 클수록), 해당 샘플의 기여도가 커진다
- 기본 광선 값 1.0에서 현재 샘플의 투과율을 빼서 구한다
$$O_i = 1 - e^{-\sigma_i \delta_i}$$
• $O_i$값이 크면 -> 현재 샘플이 빛을 적게 투과함 (불투명)
• $O_i$값이 작으면 -> 현재 샘플이 빛을 많이 투과함 (투명)
| 샘플링 위치 | 불투명도($O_i$) |
| t1 | $1 - e^{-0.2 \times 0.5} \approx 0.095$ |
| t2 | $1 - e^{-0.4 \times 0.5} \approx 0.181$ |
| t3 | $1 - e^{-0.8 \times 0.5} \approx 0.329$ |
| t4 | $1 - e^{-0.3 \times 0.5} \approx 0.141$ |
3. 기여도 / 최종 색상 계산
누적투과율과 각 샘플의 불투명도를 곱해 샘플별 기여도가 계산된다
$$T_i \cdot (1 - e^{-\sigma_i \delta_i})$$
| 샘플링 위치 | $T_i \cdot (1 - e^{-\sigma_i \delta_i})$ |
| t1 | $0.90 \times 0.095 = 0.086$ |
| t2 | $0.71 \times 0.181 = 0.128$ |
| t3 | $0.44 \times 0.329 = 0.145$ |
| t4 | $0.38 \times 0.141 = 0.053$ |
샘플별 기여도와 색상을 곱한 값들을 누적해 최종 색상값이 만들어진다
$$C(x) = \sum_{i} T_i \cdot (1 - e^{-\sigma_i \delta_i}) \cdot c_i$$
- $C(x) \approx (170, 90, 100)$
- 최종적으로 빨강과 파랑이 섞인 보라색 계열 색상이 만들어진다
Volume Rendering(ray-casting)을 하는 이유
✅ 3D 볼륨 데이터를 전체적으로 표현할 수 있음
✔️ 기존 표면 기반 렌더링(Surface Rendering)은 객체의 표면만 표현할 수 있었음.
✔️ 하지만, 볼륨 데이터는 내부 정보까지 포함해야 하므로, 3D 공간 내 모든 위치에서 밀도(𝜎) 값을 저장하는 방식이 필요함.
✔️ 볼륨 레이 캐스팅은 3D 볼륨 데이터를 직접 샘플링하여, 내부까지 시각적으로 표현할 수 있음.
✅ 투명한 구조(Opacity)와 색상(RGB) 정보를 조합하여 렌더링 가능
✔️ 기존의 표면 기반 렌더링 방식은 불투명한 물체를 렌더링하는 데 적합했지만, 반투명한 볼륨 데이터를 표현하는 데 한계가 있었음.
✔️ 볼륨 데이터는 연기, 구름, 의료 스캔 데이터처럼 부분적으로 반/투명한 구조를 가질 수 있음.
✔️ 볼륨 레이 캐스팅은 밀도(𝜎) 값에 따라 빛이 얼마나 흡수되고, 얼마나 투명한지를 계산하여 사실적인 볼륨 표현을 가능하게 함.
📌 활용 예시:
• 연기, 구름 렌더링 → 밀도 변화에 따라 자연스럽게 투명도를 조절하여 표현 가능.
• 유체 시뮬레이션(Fire, Smoke) → 입자가 섞여 있는 환경에서 자연스러운 시각적 효과를 구현.
• AR/VR 의료 영상 → MRI/CT 데이터에서 내부 장기 구조를 자연스럽게 표시.
최근에는 NeRF등의 3D 장면을 재구성하는 기술 등에도 활용되고 있는데 이건 다음에 정리할 예정
'논문 & 기술' 카테고리의 다른 글
| DeepSORT (5) | 2025.05.01 |
|---|---|
| YOLO (0) | 2025.05.01 |
| Faster R-CNN (3) | 2025.04.23 |
| R-CNN (1) | 2025.04.17 |
| NERF : Representing Scenes as Neural Radiance Fields for View Synthesis (0) | 2025.03.26 |